1️⃣ 시계열 자료와 확률과정
1. 확률과정(Stochastic process)
① 시계열 자료
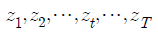
- 시간을 통해서 순차적으로 발생한 실측값
② 확률과정
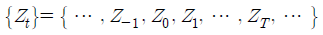
- 시점 t에 대응되는 확률변수들의 집합
2. 정상성
① 정의 및 특징
- 정의 : 시계열의 확률적인 성질들이 시간의 흐름에 따라 불변
- 특징
- 뚜렷한 추세가 없음. 즉, 시계열의 평균이 시간 축에 평행
- 시계열의 진폭(변동)이 시간의 흐름에 따라 일정
- 시계열 자료의 과거와 미래의 상관관계가 시간의 흐름에 따라 일정

② 평균, 분산, 자기공분산
- 정상성은 평균, 분산, 자기공분산이 시점 t에 관계없이 일정
- 평균 μ 는 모든 시점에서 일정
- 분산 σ^2 는 모든 시점에서 일정
- 자기공분산이 시차(time lag, k = t - s)에만 의존
③ 정상성을 갖는 시계열 자료 그림

- 추세를 갖지 않는다
- 변동(분산)이 증가하거나 감소하지 않는다.
- 일정한 형태의 자기상관성을 가진다.
2️⃣ 자기상관함수
1. 자기상관계수(AutoCorrelation Function : ACF)
- 일반적인 시계열 자료는 현재의 상태가 과거 및 미래의 상태와 밀접한 관계 를 갖고 있음
- 즉, 자기상관관계를 갖음.
- 자기상관계수 : 시간에 따른 상관 정도

- 성질

2. 표본자기상관함수(SACF)
- 시계열 자기상관계수
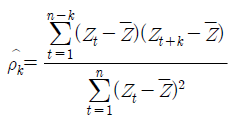
- 이론적인 성질에 의해 |p_hat| > 2 / n 이면 H_0 : p_k = 0 이 기각되어 Z_t 들은 시차 k 에서 자기상관관계가 존재
3. 부분자기상관계수(Partial Autocorrelation Coefficients, PACF)

- 자기상관과 부분자기상관

3️⃣ 백색잡음과정
1. 정상과정 : 백색잡음과정
- e_t들이 서로 독립이고 평균 0 , 분산 σ^2 을 갖는 확률변수라고 할때
e_t가 백색잡음과정 WN(0, σ^2) 을 따름
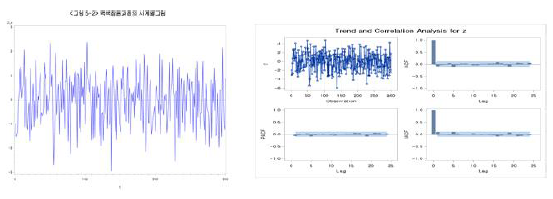
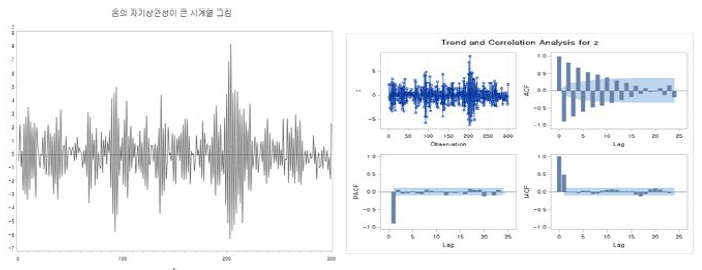
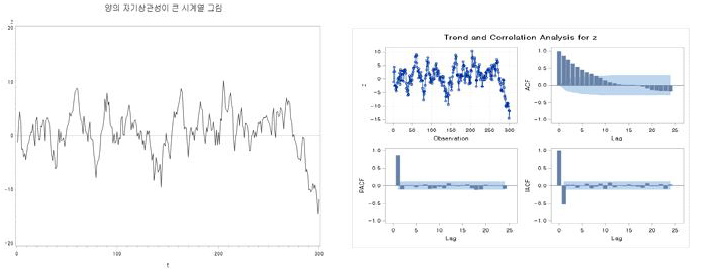
2. 비정상과정
① 절편이 없는 확률보행과정

- e_t가 백색잡음과정 WN(0, σ^2) 을 따르고, 위와 같이 정의되는 확률과정 {Z_t}를 확률보행과정이라 함

② 절편이 있는 확률보행과정

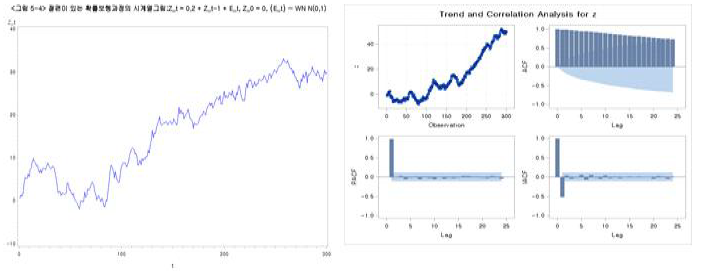
728x90
반응형
'Statistics > 시계열분석' 카테고리의 다른 글
| 2. 전통적 방법 : 시계열 데이터 구성요소(추세, 순환, 계절, 우연변동) (0) | 2022.07.29 |
|---|---|
| 1. 시계열 분석 개요 및 데이터 다루기 (0) | 2022.07.25 |
