1. 의미
- 크기(magnitude)와 방향(direction)을 가진 물리량, 차원의 공간에 존재
- (대수적 정의) 수 또는 함수의 나열
- 보통 데이터의 묶음(tuple), 열과 행 존재
- 데이터 레코드 하나를 단독으로 벡터로 나타낼 때는 열 하나로 표시
2. 단위 벡터
- 같은 벡터라도 좌표가 다를 수 있다.
- 길이가 1인 벡터, 방향o, 크기 영향x
- 정규화(normalizing) : 벡터를 단위 형태로 변환하는 것
3. 벡터의 크기 = 길이 = norm
from scipy import linalg
linalg.norm(a) # norm- L1 : 컴퓨터 비전에서 주로 씀 |x| = a+b+c
- L2 : K-평균 클러스터링과 K-최근접 |x| = sqrt(a+b+c)
linalg.norm(a, ord = 1)
linalg.norm(a, ord = 2)
4. 위치 벡터
- 원점이 시작점에 있지 않은 벡터를 원점이 시작점인 벡터들로 표현
5. 영 벡터
- 모든 성분이 0
- 필요성 : 벡터 공간 내에 존재하는 모든 벡터는 선형 결합(linear combination)으로 만들 수 있어야 함.
np.zeros()6. 인공지능에서 벡터의 의미
- 숫자의 집합 및 배열
- 특성 벡터(feature vector)
- 필요성 : 1) 인공신경망에서 입력 데이터는 숫자 데이터만 가능
2) 유사 데이터를 분류하는 데 사용(clustering)
7. 벡터의 내적(dop product, inner product)
- 벡터를 숫자처럼 곱하는 것. 임의의 두 벡터에서 스칼라 값을 생성
- 한 벡터의 크기를 구하거나 두 벡터 사이의 거리를 측정
1) 인공지능에서의 내적
- 데이터 간 유사도를 측정할 때, 그 기준은 벡터 간 거리를 이용 => 내적 사용
- 예) k-최근접 이웃 역시 데이터 간 간 거리를 측정, 가장 가까운 벡터끼리 그룹 형성하여 데이터 분류
np.dot(A, B)
8. 벡터의 외적(outer product)
- 3차원 공간에 있는 벡터 간 연산(벡터곱)
- 방향o, 크기o
np.cross(a,b)
9. 직교 벡터(orthogonal vector) -> 알고리즘 원리 이해에 필요
- 두 벡터 사이의 각도가 90도
- SVM : 주어진 데이터가 어떤 범주에 속할지 판별하는 분류 모델로, 패턴 인식이나 자료 분석에 주로 사용
10. 벡터 거리(distance)
- 추천 시스템 : 아이템이나 사용자 간 유사성 개념을 기반으로 동작
- 문서의 유사도 : 자연어 처리 분야, 검색 엔진이나 클러스터링 모델에서 많이 사용
① 유클리드 거리(Euclidean distance) ***
- 두 벡터 간 직선 거리
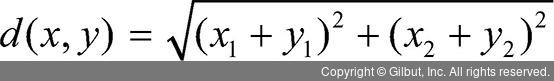
from scipy.spatial import distance
distance.euclidean(p1, p2)
② 맨해튼 거리(manhattan distance)
- 사각형 격자로 된 지도에서 출발점부터 도착점까지 가로지르지 않고 갈 수 있는 최단 거리를 구하는 공식
d(x, y) = |x1 - x2| + |y1 - y2|
def manhattan(x, y):
return sum(abs(a-b) for a,b in zip(x,y))
③ 코사인 유사도(cosine similarity)
- 두 벡터의 방향이 같을수록 벡터가 비슷하다고 간주하여 두 벡터 간의 각인 코사인 값을 말함
- 각이 작을 수록 유사도가 높고, 클수록 유사도는 낮다.

Last Updated. 2025.06.18
🔖 참고 자료
[참고도서] : 모든 이미지의 저작권은 해당 링크에 있습니다.
https://thebook.io/080246/part03/ch10/unit18/03/
'ML | DL' 카테고리의 다른 글
| Data Scientist vs AI Engineer (1) | 2025.07.10 |
|---|---|
| [AICE Associate] 문제 유형 별 정리 (2) | 2025.06.27 |
| [인공지능 기초수학] #2. 스칼라, 벡터, 행렬, 텐서 (0) | 2025.06.18 |
| [인공지능 기초수학] #1 미분법 - 오차역전파 (0) | 2025.06.18 |
| 머신러닝과 딥러닝 개념 총정리 (2) | 2025.06.17 |
